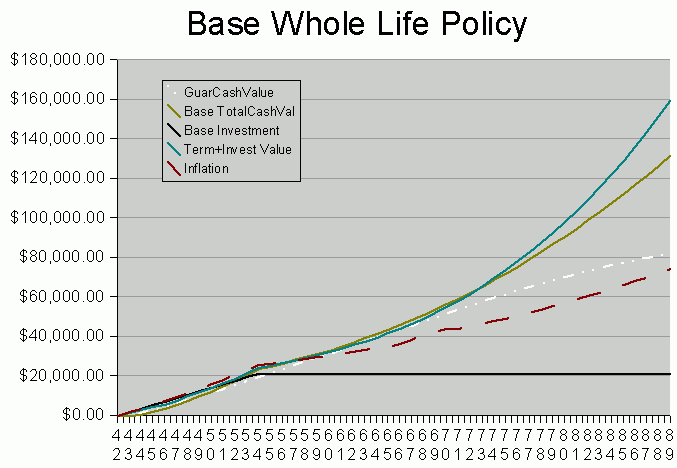
Let us see what New York Life predicted for my policy.  The insurance Cash Value Curve is straight from NYL, with no modifications made by me.
Let us examine this graph line by line, beginning with the topmost one.  If you wish to reference the graph while reading the description, click it.  A smaller version will appear in a different window, one that stays in front.  Don't worry!  It will go away when you click it closed.

• The solid turquoise line represents the the minimum T+I strategy.
  This model is mine, not part of the NYL illustration.  It represents an earnings rate of about 6.75% on the invested portion.  Up to age 71, it must use $485/year to pay for term insurance.  After that, the load is removed, and you can see that then it finally takes a permanent lead.
  
  
• The solid brown line represents projected Total Cash Value.
  This line starts low but catches up with min T+I for a few years.  It takes it about 10 years to cross-over the cost line and 15 years to cross-over inflation.  The curve is a bit misleading during the first few years.  Should I need to "lapse the policy" (cancel it), the premium paid for the year will be pro-rated with the number of months that have passed.  This pro-rated value is not represented by the curve.  (Should I die instead, the premium will also be pro-rated.  In case of death, the pro-rating is a proportional return for the policy months I happen to be dead.  In case of simple lapse, the pro-rating is less generous but still significant.)
  
  
• The dashed and dotted white line represents Guaranteed Cash Value.
  Even if there are no dividends reinvested in the policy, it will still gain Guaranteed Cash Value (GCV) each year, beginning at the end of the third year.  The policy's death benefit would remain flat at $100,000.  This could happen in two ways:
  • NYL does not meet its earnings projections.
    In this event, the policy might earn dividends from zero dollars to anything less than the projected amount.  Should a significant projection failure occur, the insurance company loses a lot of credibility to its customers, and many will choose to lapse (cancel) their current policies.  In my opinion, it would be similar to a Money Market Mutual Fund which cannot sustain its earnings and has to allow price per share to drop below $1.  "Breaking the buck" could happen in such a fund, but the loss of prestige (and loss of people who choose to invest in it) have made such an event unlikely among any of the major mutual fund families.
  • The policy owner chooses not to reinvest his dividends.
    The default option for dividends is to use them to purchase Paid-Up Additions.  This additional insurance is the means used to keep dividends and their cash value within the policy, and which raises the death benefit over time.  The other options are:
    1. Get a check from NYL each year.
       You can do anything you want with the dividend money.  Throw a party, even.  Or perhaps try a sixth insurance strategy -- "buy Whole Life, and invest the dividends yourself".  (I have not modeled this one.)  For tax purposes, the dividend check is considered a partial rebate of your premium, and it is not initially taxable.  After many years, the dividend may be higher than your premium, in which case the difference would be considered taxable income.
    2. Have NYL put the dividend into an interest-bearing account.
       I am not sure why anyone would want to keep the money with NYL but not reinvest it back into their policy, but it is one of my options.
    3. Use the dividend as partial payment of next year's premium.
       I could have begun lowering my premium payments beginning the third year.  The dividend would be part of the next year's premium, and I would write a check for the difference.  No "compounding" of the dividend amounts would occur over time; that is, re-invested dividends would not be earning dividends of their own.  Thus it would take much longer than 12 years (the projected time under the reinvest option) to get to the point where dividends and other accumulated value could fully pay the premium.
       
  
  
• Inflation is the dashed red line in the center.
  
  
• The solid black line represents out of pocket dollars.
  This is expected to be $1764/year for the first 12 years.  After that, NYL predicts, but does not guarantee, that policy earnings will be sufficient to pay the premium.

Fred the Actuary predicts that I am going to die around age 79.  I hope he is wrong, and I let the graph continue to age 89 just to spite him.

Has a "buy term and invest the difference" strategy been shown to be the best to follow?  When minimal money goes into the whole life insurance policy, it would seem so.

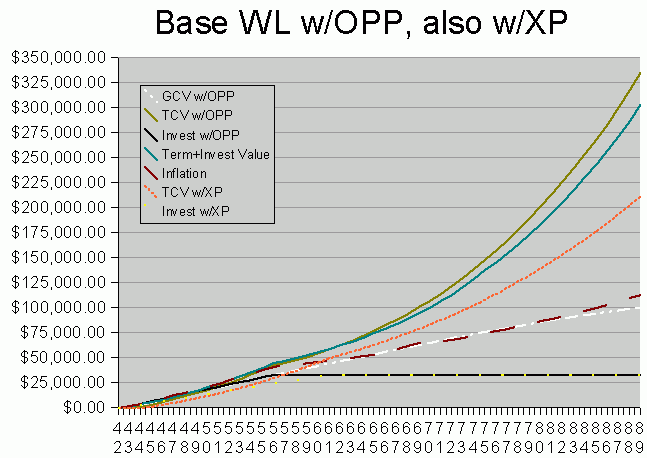
Now let us make things more interesting.  Modify NYL's illustration with my front-loading of Paid Up Additions ("PUA", aka "OPP" for "Option to Purchase Paid-Up Additions").
This chart is crowded during the early years.  One reason for this is that it displays both a front-loaded and a back-loaded case for the same out-of-pocket dollars.  I had done the front-loaded (OPP) case first, but then I began to wonder what would happen if someone simply kept paying the annual premiums until such time as no sell-backs of PUA would be necessary.  This resulted in the Extra Payment (XP) lines.

• The solid brown line represents Total Cash Value for the OPP strategy.
  This is my intended strategy and primary model.  Basically I plan to invest $2400/year for 12 years.  This is about 1/3 more than my actual premium payment of $1764.  In year 13, $2200 is paid, and in year 14, $2000 is paid.  After that, the policy is expected to be fully self-sustaining.  (This is the same investment schedule as the max Term+Invest curve.)

  Cross-over with cost occurs at year 9, and with inflation at year 12.  Cross-over with the T+I strategy occurs at year 21.  The drain of term payments eventually cost T+I its lead.  In exact opposition, the high LIV (linear increase in value) of the OPP strategy adds hundreds of dollars of cash value each year.
  
  

• The solid turquoise line represents the "max" T+I strategy.
  Using the same investment schedule as OPP, this strategy keeps a small lead for two decades.  Proportionally, the $485/year spent for term insurance is smaller than for min T+I, and at age 71 there is barely a ripple when this term load is removed.
  
  
• The dashed orange line represents Total Cash Value in the XP strategy.
  The normal premium payment is made for about 7 more years than in the Base Policy strategy (18 years at $1764, with $1248 paid in 19th year).  The sum of premiums is still $33,000 as in OPP, but you can see that spreading it out over more years reduces overall gain.  The major advantage of this strategy over the Base Policy is that dividends are fully able to make the premium payments when the out-of-pocket period stops.  In Base Policy, value already accumulated within the policy had to be sold back for several years; the dividends were not high enough after just 12 years to fully cover the cost of premiums.
  
  
• Inflation is again the dashed red line in the center.
  For simplicity, I only show inflation for the OPP case, not the XP case.  The XP investment would cross-over it's true inflation line much sooner than this chart would indicate.
  
  
• The dashed and dotted white line represents Guaranteed Cash Value.
  It applies to the OPP strategy, not the XP.  When I directly purchase paid-up additions, there is a corresponding increase in guaranteed value, but making extra premium payments does not modify any guaranteed values.  So guaranteed value for the XP strategy is exactly the same as it is for the Base WL strategy in the first chart.
  
  
• The black line which goes horizontal is out-of-pocket dollars.
  This is at a total investment of $33,500 compared to $21,168 in the Base Policy case above.
  
  
• The yellow dots are out-of-pocket dollars in the XP strategy.
  They represent a linear $1764/year until $33,000 is expended.

If this model is correct, my hypothesis is verified.
Front-loading cash into the back-loaded earning design of my policy results in significant gain improvement.  Here is a tabular summary of the modeled strategies:

Model Summary, Age 42 thru 79
Strategy	Invested -> Value	Absolute Gain	Inflation Gain
T+I min	$21,168 ->  $92,671	338%	$55,411    67%
Base CV	$21,168 ->  $86,772	310%	$55,411    57%
T+I max	$33,000 -> $174,070	427%	$84,338   106%
CV w/XP	$33,000 -> $133,349	304%	$79,078    69%
CV w/OPP	$33,000 -> $190,159	476%	$84,338   125%

(There is no T+I model mate for the XP case.  Comparing it with the Base Policy case is instructive, however.  Base "beats" XP in absolute gain, but loses to XP in both reality and inflation gain.  That is because by year 12, the Base Policy case has "invested" all of its money, and every year after that, the entirety is subject to inflation.  However, it is not until policy year 19 that all of the XP investment has been made.  Thus the total effect of inflation is less than the Base case.)

Why does the OPP case beat its T+I mate, but the Base Policy case lose to its mate?  The return on the Base Policy case is damaged during nine years of PUA sell-backs.  This saves out of pocket expenses, but hinders the "investment" properties of the policy.  On the other hand, the OPP case intentionally overfunds the policy.  Not only does nothing need to be sold back, but gain begins from the very first policy year.

There is no magic, or "cheating", or getting money for nothing.  Given the choice to wait years for gains to begin to accrue or begin getting a return right away, it just made sense not to wait.  Ricky says:

By listening to him this time and not accepting the extremely high losses the first two years, I seem to be on track to something better.  Thanks, Ricky!