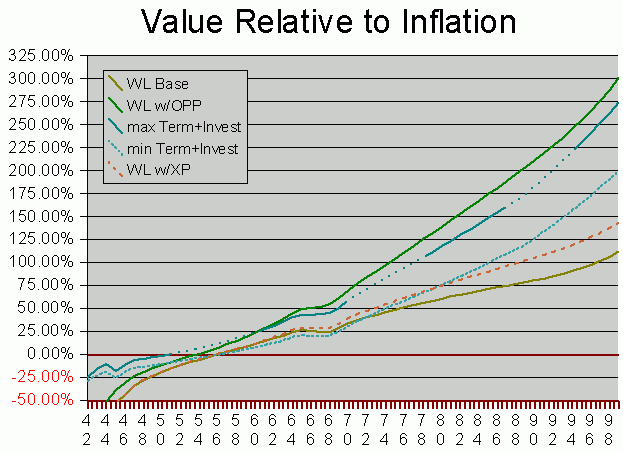
The Black Box Annual Gain curve showed one personality aspect for the investment strategies, this curve shows another. Instead of focusing on the year-to-year gains, this view steps back and watches how the total investment is doing in terms of real value. If the investment is at the 0% line, it is keeping up with inflation. A loaf of bread may cost more 20 years from now, but investments that keep up with inflation have the added value to pay for this increase without noticing. Investment strategies which map above the 0% line are gaining real value. In a sense, that loaf of bread is getting cheaper, even though its cost is going up. Here is the formula for Inflation Wave Ratio, Cash Value:
-----------------------------------
totalInflatedCost
Let us look at each strategy, beginning again from the top right. Click the curve above to get a smaller version in a different window. You can compare it as you read the following analysis.
- The solid green line represents Total Cash Value (TCV) of the OPP strategy.
($33,000 is put into the policy over 14 years.) In this strategy, from the first policy years I am exercising my Option to Purchase Paid-up-insurance. Presuming my model for this strategy is correct, doing so clearly pays off in the long run. Even so, it takes 13 years to get ahead of the inflation line and be considered any kind of useful investment. Finally in the 21st year it overtakes the max T+I curve.
There is a reason all the curves flatten out for a few years in the center. For most future years, the model uses a 3% inflation rate. For past years (beginning 1996) it uses actual inflation rates. The "flat" years, however, model a 6% inflation rate; I was curious to see what the impact of a higher inflation rate would be.
- The long-dashed and dotted turquoise line represents the "max T+I" case.
($33,000 is invested for 14 years; $485/year is deducted to purchases term insurance for 30 years.) For the first 21 years, it is the leading curve. However it begins to lose ground after year 14. In the Whole Life w/OPP case, the cost of insurance is minor, at least until age 70 or so. Two things then occur at about the same time. The Term+Invest strategy completes its 30-year term period, and no longer has to not-invest $485/year. Within the Whole Life policy, cost of insurance becomes significant. This can be seen on the BBAG curve, previous page.
To give you an absolute reference, by age 89 this case has a value of $304,000 and the OPP a value of $336,000.
- The dotted turquoise line represents the "min T+I" case.
($21,168 total is invested for 12 years; $485/year is deducted to purchase term insurance for 30 years.) Once the term period stops, its gain easily surpasses that of the Base Policy case. In the long term, this is even a more efficient strategy than the "Base Policy with XP" case -- in absolute dollars, the XP case stays ahead, but it used $33,000 out-of-pocket dollars to get there.
- The dashed orange line represent TCV for the XP strategy.
($33,000 is put into the policy over 19 years.) While it earns more absolute dollars than the Base Policy case, the efficiency of those earnings is only slightly better. That is not to say the absolute dollars don't matter; by age 89 XP has a TCV of $212,000, Base Policy has a TCV of $132,000, and the "min T+I" has a value of $160,000.
Why does efficiency of "XP" dollars begin to exceed "Base" dollars? Examination of the models shows that there are three annual sources of gain in both cases. Guaranteed Cash Value increases each year exactly the same in both. Dividends increase in both, but the dividend rate is the same, so this does not affect efficiency. The third source of gain eventually becomes significant -- "linear increase in value" (LIV) of the Paid Up Additional insurance purchased by dividends. It takes years for the extra LIV to noticeably improve efficiency over the Base Policy case, but you can see that it eventually does.
The OPP case excels for two reasons. In the first place, more money is put into the policy earlier, increasing dividends and the LIV earned on the PUA purchased with those dividends. Secondly, OPP adds a fourth source of annual earnings -- LIV earned on the PUA purchased with OPP dollars.
- The solid brown line represent TCV for the Base Policy case.
($21,168 is put into the policy over 12 years.) Two things are important about this curve. The first is that it is probably the strategy which most purchasers of participating whole life insurance will follow. The second is that it does eventually become an "investment" -- total cash value begins to exceed its inflated cost. It takes 15 years for this to become true, however. (It only took 11 years to exceed absolute cost, but until year 15, less loaves of bread can be purchased than before you started.)
"I don't see inflation!"
It is there; you are riding inflation, remember? Every strategy
is ratiod against inflation, putting it exactly at the 0% line.
There are actually three inflation curves involved.
Each strategy is ratiod against its appropriate inflation curve.
Depending on how much money was invested
for each year, the inflation curve is different. For example,
$30,000 invested up front would be inflated 3% of the whole amount each
year. All of it will increase in a compounded manner from the second
year on. But if $3,000 were invested each year for 10 years, the
total effect of inflation will be less. E.g., the $3,000 invested in
year 8 does not have many years of inflation history and compounding behind it.